Bloch oscillation in a dynamically modulated ring resonator
1using LatticeModels, Plots; LM = LatticeModels
2using QuantumOptics
3using Plots.Measures
4
5default(fmt=:png,
6 fontfamily="computer modern", titlefont="computer modern", tickfont="computer modern";
7 linewidth=2, legend_position=:best
8 )
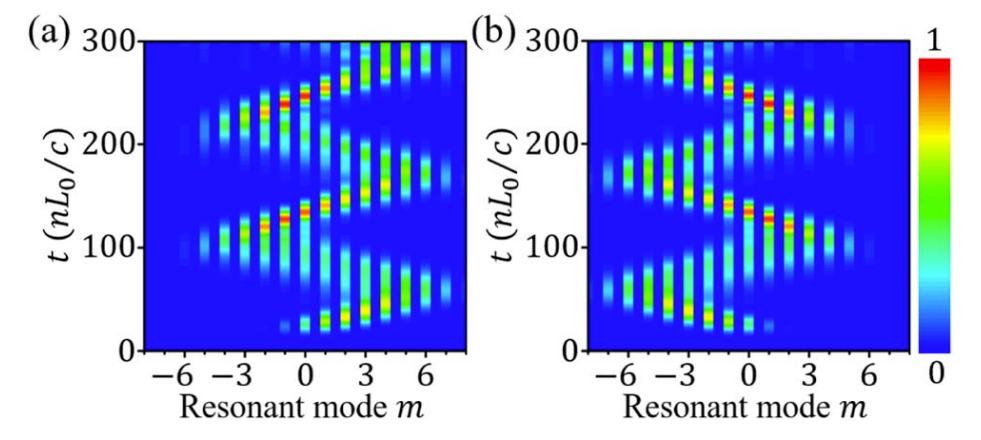
We want to reproduce the Bloch oscillation in a ring resonator. A ring resonator with a dynamic refractive index modulation can exhibit Bloch oscillation of light along the frequency axis, as a result of an effective force for photons induced by the modulation, as is shown in Yuan et al (2016).
Furthermore, we want to show that one can deduce directional transport on the frequency axis by switching the detuning periodically.
We will implement the model ad deduced in Yuan et al (2016): $$ \tilde{H}=g \sum_m\left(c_m^{\dagger} c_{m+1}+c_{m+1}^{\dagger} c_m\right)+\sum_m m \Delta(t) c_m^{\dagger} c_m, $$ where $m$ is the resonant mode of the waveguide in the resonator, $g$ is the strength of the modulation, and $\Delta$ is the detuning of the resonant frequency of the waveguide from the modulation frequency.
We start by implementing a lattice of 100 sites, i.e., we consider 100 modes of the waveguide. The lattice will have reflective boundary conditions. Furthermore, the tight binding system has one particle and a chemical potential of zero. No extra particles can be added to the system.
1size=100
2lattice = SquareLattice(size, 1)
3x_basis = PositionBasis(0, size, size)
4
5sample = Sample(lattice, boundaries=BoundaryConditions(1 => true, 2 => true))
6system = System(sample, μ=0.0, statistics=LM.OneParticle)
LatticeModels.FilledZones{Sample{Nothing, SquareLattice{2}, Nothing, BoundaryConditions{Tuple{TwistedBoundary, TwistedBoundary}}}}(Sample{Nothing, SquareLattice{2}, Nothing, BoundaryConditions{Tuple{TwistedBoundary, TwistedBoundary}}}(nothing, SquareLattice{2}((100, 1), LatticeModels.Bravais{2, 1}([1.0 0.0; 0.0 1.0], [0.0; 0.0;;]), Bool[1, 1, 1, 1, 1, 1, 1, 1, 1, 1 … 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]), BoundaryConditions{Tuple{TwistedBoundary, TwistedBoundary}}((TwistedBoundary(1, 0.0), TwistedBoundary(2, 0.0))), nothing), 0.0, LatticeModels.OneParticle)
We implement the time dependent Hamiltonian where switch the detuning periodically between -$\Delta$ and +$\Delta$ with a period of $T=1$.
1g = 2; Δ = 2
2function h(t, g, Δ; switch = t -> isodd(floor(t)) ? -1 : 1)
3 build_hamiltonian(lattice,
4 lattice .|> (site -> Δ* switch(t)*site.coords[1]),
5 g => SiteOffset(axis=1)
6 )
7end
8H0 = h(0, g, Δ)
Hamiltonian(dim=100x100)
basis: LatticeBasis{SquareLattice{2}}(100, SquareLattice{2}((100, 1), LatticeModels.Bravais{2, 1}([1.0 0.0; 0.0 1.0], [0.0; 0.0;;]), Bool[1, 1, 1, 1, 1, 1, 1, 1, 1, 1 … 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]))
sparse([1, 2, 1, 2, 3, 2, 3, 4, 3, 4 … 97, 98, 97, 98, 99, 98, 99, 100, 99, 100], [1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 6, 7, 7, 7, 8, 8, 8, 9, 9, 9, 10, 10, 10, 11, 11, 11, 12, 12, 12, 13, 13, 13, 14, 14, 14, 15, 15, 15, 16, 16, 16, 17, 17, 17, 18, 18, 18, 19, 19, 19, 20, 20, 20, 21, 21, 21, 22, 22, 22, 23, 23, 23, 24, 24, 24, 25, 25, 25, 26, 26, 26, 27, 27, 27, 28, 28, 28, 29, 29, 29, 30, 30, 30, 31, 31, 31, 32, 32, 32, 33, 33, 33, 34, 34, 34, 35, 35, 35, 36, 36, 36, 37, 37, 37, 38, 38, 38, 39, 39, 39, 40, 40, 40, 41, 41, 41, 42, 42, 42, 43, 43, 43, 44, 44, 44, 45, 45, 45, 46, 46, 46, 47, 47, 47, 48, 48, 48, 49, 49, 49, 50, 50, 50, 51, 51, 51, 52, 52, 52, 53, 53, 53, 54, 54, 54, 55, 55, 55, 56, 56, 56, 57, 57, 57, 58, 58, 58, 59, 59, 59, 60, 60, 60, 61, 61, 61, 62, 62, 62, 63, 63, 63, 64, 64, 64, 65, 65, 65, 66, 66, 66, 67, 67, 67, 68, 68, 68, 69, 69, 69, 70, 70, 70, 71, 71, 71, 72, 72, 72, 73, 73, 73, 74, 74, 74, 75, 75, 75, 76, 76, 76, 77, 77, 77, 78, 78, 78, 79, 79, 79, 80, 80, 80, 81, 81, 81, 82, 82, 82, 83, 83, 83, 84, 84, 84, 85, 85, 85, 86, 86, 86, 87, 87, 87, 88, 88, 88, 89, 89, 89, 90, 90, 90, 91, 91, 91, 92, 92, 92, 93, 93, 93, 94, 94, 94, 95, 95, 95, 96, 96, 96, 97, 97, 97, 98, 98, 98, 99, 99, 99, 100, 100], ComplexF64[2.0+0.0im, 2.0+0.0im, 2.0-0.0im, 4.0+0.0im, 2.0+0.0im, 2.0-0.0im, 6.0+0.0im, 2.0+0.0im, 2.0-0.0im, 8.0+0.0im … 194.0+0.0im, 2.0+0.0im, 2.0-0.0im, 196.0+0.0im, 2.0+0.0im, 2.0-0.0im, 198.0+0.0im, 2.0+0.0im, 2.0-0.0im, 200.0+0.0im], 100, 100)
As initial condition, we choose a Gaussian lattice density profile with a width of $\sigma=5$:
1ψx = gaussianstate(x_basis, div(size, 3), 0.0, 5)
2ψl = Ket(H0.basis_r, ψx.data)
3
4P0 = Operator(ψl.basis, ψl.data * ψl.data')
5d = lattice_density(P0)
6plot(d.values)
1g = 2; Δ = 2
2density_rec = []
3@evolution show_progress=false {H := h(t, g, Δ), P0 --> H --> P} for t in 0:0.01:20
4 d = lattice_density(P) .|> real
5 push!(density_rec,d.values)
6end
7p1 = heatmap(hcat(density_rec...)', xlabel="lattice site", ylabel="time", title="Δ=±$(Δ)", colorbar=false)
8
9density_rec = []
10@evolution show_progress=false {H := h(t, g, Δ, switch= x-> 1), P0 --> H --> P} for t in 0:0.01:20
11 d = lattice_density(P) .|> real
12 push!(density_rec,d.values)
13end
14p2 = heatmap(hcat(density_rec...)', xlabel="lattice site", ylabel="time", title="Δ=$(Δ)", colorbar=false)
15
16density_rec = []
17@evolution show_progress=false {H := h(t, g, Δ, switch= x-> -1), P0 --> H --> P} for t in 0:0.01:20
18 d = lattice_density(P) .|> real
19 push!(density_rec,d.values)
20end
21p3 = heatmap(hcat(density_rec...)', xlabel="lattice site", ylabel="time", title="Δ=-$(Δ)");
1l = @layout [a b c{0.42w}]
2plot(p1, p2, p3, layout=l, size=(1200,400), plot_title="Normalised lattice density",
3 margin=5mm, plot_titlevspan=0.1)
4# savefig(plotsdir("lattice_density.png"))
1plot(p2, xlim=(20, 50))
1function evolution_operator(h, t)
2 H = h(t)
3 ev_op = Operator(basis(H), H.data)
4 LM.evolution_operator!(ev_op, H, t)
5 return ev_op
6end
7time_hamiltonian = t -> h(t, 2, 2)
8ev_op = evolution_operator(time_hamiltonian, 2.1)
Operator(dim=100x100)
basis: LatticeBasis{SquareLattice{2}}(100, SquareLattice{2}((100, 1), LatticeModels.Bravais{2, 1}([1.0 0.0; 0.0 1.0], [0.0; 0.0;;]), Bool[1, 1, 1, 1, 1, 1, 1, 1, 1, 1 … 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]))sparse([1, 2, 3, 4, 5, 6, 1, 2, 3, 4 … 97, 98, 99, 100, 95, 96, 97, 98, 99, 100], [1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 26, 26, 26, 26, 26, 26, 26, 26, 26, 26, 26, 27, 27, 27, 27, 27, 27, 27, 27, 27, 27, 27, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 31, 31, 31, 31, 31, 31, 31, 31, 31, 31, 31, 32, 32, 32, 32, 32, 32, 32, 32, 32, 32, 32, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 34, 34, 34, 34, 34, 34, 34, 34, 34, 34, 34, 35, 35, 35, 35, 35, 35, 35, 35, 35, 35, 35, 36, 36, 36, 36, 36, 36, 36, 36, 36, 36, 36, 37, 37, 37, 37, 37, 37, 37, 37, 37, 37, 37, 38, 38, 38, 38, 38, 38, 38, 38, 38, 38, 38, 39, 39, 39, 39, 39, 39, 39, 39, 39, 39, 39, 40, 40, 40, 40, 40, 40, 40, 40, 40, 40, 40, 41, 41, 41, 41, 41, 41, 41, 41, 41, 41, 41, 42, 42, 42, 42, 42, 42, 42, 42, 42, 42, 42, 43, 43, 43, 43, 43, 43, 43, 43, 43, 43, 43, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 45, 45, 45, 45, 45, 45, 45, 45, 45, 45, 45, 46, 46, 46, 46, 46, 46, 46, 46, 46, 46, 46, 47, 47, 47, 47, 47, 47, 47, 47, 47, 47, 47, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 49, 49, 49, 49, 49, 49, 49, 49, 49, 49, 49, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 51, 51, 51, 51, 51, 51, 51, 51, 51, 51, 51, 52, 52, 52, 52, 52, 52, 52, 52, 52, 52, 52, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 54, 54, 54, 54, 54, 54, 54, 54, 54, 54, 54, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 55, 56, 56, 56, 56, 56, 56, 56, 56, 56, 56, 56, 57, 57, 57, 57, 57, 57, 57, 57, 57, 57, 57, 58, 58, 58, 58, 58, 58, 58, 58, 58, 58, 58, 59, 59, 59, 59, 59, 59, 59, 59, 59, 59, 59, 60, 60, 60, 60, 60, 60, 60, 60, 60, 60, 60, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 62, 62, 62, 62, 62, 62, 62, 62, 62, 62, 62, 63, 63, 63, 63, 63, 63, 63, 63, 63, 63, 63, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 64, 65, 65, 65, 65, 65, 65, 65, 65, 65, 65, 65, 66, 66, 66, 66, 66, 66, 66, 66, 66, 66, 66, 67, 67, 67, 67, 67, 67, 67, 67, 67, 67, 67, 68, 68, 68, 68, 68, 68, 68, 68, 68, 68, 68, 69, 69, 69, 69, 69, 69, 69, 69, 69, 69, 69, 70, 70, 70, 70, 70, 70, 70, 70, 70, 70, 70, 71, 71, 71, 71, 71, 71, 71, 71, 71, 71, 71, 72, 72, 72, 72, 72, 72, 72, 72, 72, 72, 72, 73, 73, 73, 73, 73, 73, 73, 73, 73, 73, 73, 74, 74, 74, 74, 74, 74, 74, 74, 74, 74, 74, 75, 75, 75, 75, 75, 75, 75, 75, 75, 75, 75, 76, 76, 76, 76, 76, 76, 76, 76, 76, 76, 76, 77, 77, 77, 77, 77, 77, 77, 77, 77, 77, 77, 78, 78, 78, 78, 78, 78, 78, 78, 78, 78, 78, 79, 79, 79, 79, 79, 79, 79, 79, 79, 79, 79, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 81, 81, 81, 81, 81, 81, 81, 81, 81, 81, 81, 82, 82, 82, 82, 82, 82, 82, 82, 82, 82, 82, 83, 83, 83, 83, 83, 83, 83, 83, 83, 83, 83, 84, 84, 84, 84, 84, 84, 84, 84, 84, 84, 84, 85, 85, 85, 85, 85, 85, 85, 85, 85, 85, 85, 86, 86, 86, 86, 86, 86, 86, 86, 86, 86, 86, 87, 87, 87, 87, 87, 87, 87, 87, 87, 87, 87, 88, 88, 88, 88, 88, 88, 88, 88, 88, 88, 88, 89, 89, 89, 89, 89, 89, 89, 89, 89, 89, 89, 90, 90, 90, 90, 90, 90, 90, 90, 90, 90, 90, 91, 91, 91, 91, 91, 91, 91, 91, 91, 91, 91, 92, 92, 92, 92, 92, 92, 92, 92, 92, 92, 92, 93, 93, 93, 93, 93, 93, 93, 93, 93, 93, 93, 94, 94, 94, 94, 94, 94, 94, 94, 94, 94, 94, 95, 95, 95, 95, 95, 95, 95, 95, 95, 95, 95, 96, 96, 96, 96, 96, 96, 96, 96, 96, 96, 97, 97, 97, 97, 97, 97, 97, 97, 97, 98, 98, 98, 98, 98, 98, 98, 98, 99, 99, 99, 99, 99, 99, 99, 100, 100, 100, 100, 100, 100], ComplexF64[0.9999327113815735 - 0.00820266501446412im, -0.00010093141833268 - 0.00820229703303101im, -3.364034731125e-5 + 5.5196054197e-7im, 1.88653881e-9 + 9.197841102e-8im, 1.8861004e-10 - 4.64309e-12im, 0.0 - 3.0954e-13im, -0.00010093141833268 - 0.00820229703303101im, 0.9997981396159296 - 0.01640441008695316im, -0.00016821022641636 - 0.00820110113353606im, -3.363449908477e-5 + 8.2789113194e-7im … -2.334602203862e-5 + 2.422660081674e-5im, -0.00592992240212792 - 0.00566766043323879im, 0.6879228134802496 - 0.7256911377053686im, -0.00597628217655804 - 0.00561888913526103im, -2.2117e-13 - 2.1053e-13im, 1.3091519e-10 - 1.3586203e-10im, 6.650629582e-8 + 6.356493028e-8im, -2.314663406714e-5 + 2.441743145251e-5im, -0.00597628217655804 - 0.00561888913526103im, 0.6819696779377588 - 0.731334444272082im], 100, 100)