Automatic differentiation of a recursive partition function
This tutorial demonstrates how to compute the energy of a bosonic gas in a harmonic trap using automatic differentiation.
1using ForwardDiff: derivative
2using CairoMakie, ProgressMeter
3using BenchmarkTools
4
5using Pkg; Pkg.status()
Status `/var/home/oameye/Documents/hugo-toha/content/posts/automatic_differentiation/Project.toml`
[13f3f980] CairoMakie v0.15.3
[634d3b9d] DrWatson v2.18.0
[f6369f11] ForwardDiff v1.0.1
[98b081ad] Literate v2.20.1
[92933f4c] ProgressMeter v1.10.4
1using InteractiveUtils
2InteractiveUtils.versioninfo()
Julia Version 1.10.10
Commit 95f30e51f41 (2025-06-27 09:51 UTC)
Build Info:
Official https://julialang.org/ release
Platform Info:
OS: Linux (x86_64-linux-gnu)
CPU: 12 × AMD Ryzen 5 5600X 6-Core Processor
WORD_SIZE: 64
LIBM: libopenlibm
LLVM: libLLVM-15.0.7 (ORCJIT, znver3)
Threads: 10 default, 0 interactive, 5 GC (on 12 virtual cores)
Environment:
JULIA_EDITOR = code
JULIA_VSCODE_REPL = 1
JULIA_NUM_THREADS = 10
In statistical mechanics, the partition function is a central quantity that encodes all thermodynamic information of a system. For a bosonic gas in a harmonic trap, we need to compute the energy by differentiating the logarithm of the partition function with respect to the inverse temperature $β$.
The energy of a quantum system is given by: $$ E = -\frac{\partial}{\partial \beta} \ln Z(\beta) $$ where $Z(β)$ is the partition function and $β = 1/(k_B T)$ is the inverse temperature.
Single-Particle Partition Function
The single-particle partition function for a d-dimensional harmonic oscillator: $$ z(\beta, d) = \left(\frac{e^{-\beta/2}}{1-e^{-\beta}}\right)^d $$ This accounts for the zero-point energy $(1/2)ℏω$ and the geometric series from the discrete energy levels $n·ℏω$.
1function z(β, d)
2 return (exp(-0.5*β)/(1-exp(-β)))^d
3end;
Many-Body Partition Function
For N indistinguishable bosons, the partition function is computed recursively. This accounts for the bosonic statistics where multiple particles can occupy the same quantum state. The recursive formula is: $$ Z(N, \beta, d) = \frac{1}{N} \sum_{k=1}^{N} z(k\beta, d) \cdot Z(N-k, \beta, d) $$ with the boundary condition $Z(0, β, d) = 1$.
This recursion arises from the cluster expansion of the grand canonical partition function, accounting for all possible ways to distribute N particles among the available energy levels.
1function Z(N, β, d)
2 if N == 0
3 return 1.0
4 else
5 return (1 / N) * sum(z(k * β, d) * Z(N - k, β, d) for k in 1:N)
6 end
7end;
Energy Calculation via Automatic Differentiation
The energy is computed as the negative logarithmic derivative of the partition function: $$ E = -\frac{\partial}{\partial \beta} \ln Z(\beta) $$
We implement two different approaches:
- Bosonic: Uses the full many-body partition function Z(N, β, d)
- Boltzmann: Uses the classical approximation z(β, d)^N (non-interacting)
The automatic differentiation (via ForwardDiff) computes the derivative analytically without numerical approximation, making it both accurate and efficient.
1function energy(N::Int64, β::Float64, d::Int64; type::Symbol = :boson)
2 if type == :boson
3 return -derivative(x -> log(Z(N, x, d)), β)
4 else type == :boltzmannon
5 return -derivative(x -> log(z(x, d)^N), β)
6 end
7end;
Numerical Experiment
We now compute the energy for different numbers of particles N and different inverse temperatures β. This allows us to study:
- How the energy depends on temperature $(β = 1/T)$
- How quantum statistics affect the energy for different particle numbers
- The transition from quantum to classical behavior
Parameter Space
- N: Number of particles $[1, 5, 10, 20]$
- β: Inverse temperature range $[1, 10]$ (corresponds to $T ∈ [0.1, 1]$)
- d: Dimensionality = 1 (1D harmonic oscillator)
1range2d = Iterators.product([1, 5, 10, 20], 1:0.1:10)
2mat = @showprogress map(range2d) do (N, β)
3 energy(N, β, 1)
4end
4×91 Matrix{Float64}:
1.08198 0.998961 0.931013 0.874631 0.827311 0.787217 0.75297 0.723516 0.698034 0.675874 0.656518 0.639545 0.62461 0.611431 0.599769 0.589425 0.580233 0.572048 0.564747 0.558227 0.552396 0.547174 0.542494 0.538296 0.534525 0.531138 0.528091 0.52535 0.522883 0.52066 0.518657 0.516852 0.515224 0.513755 0.51243 0.511234 0.510154 0.509179 0.508298 0.507502 0.506784 0.506134 0.505547 0.505017 0.504537 0.504104 0.503712 0.503357 0.503037 0.502747 0.502485 0.502248 0.502034 0.50184 0.501664 0.501506 0.501362 0.501232 0.501115 0.501009 0.500913 0.500826 0.500747 0.500676 0.500612 0.500553 0.500501 0.500453 0.50041 0.500371 0.500336 0.500304 0.500275 0.500249 0.500225 0.500204 0.500184 0.500167 0.500151 0.500136 0.500123 0.500112 0.500101 0.500091 0.500083 0.500075 0.500068 0.500061 0.500055 0.50005 0.500045
3.66075 3.43331 3.26044 3.12679 3.02189 2.93842 2.87119 2.81645 2.77143 2.73409 2.70286 2.67655 2.65424 2.63522 2.61891 2.60485 2.59269 2.58212 2.5729 2.56484 2.55776 2.55153 2.54604 2.54118 2.53687 2.53305 2.52965 2.52662 2.52392 2.52151 2.51935 2.51742 2.51568 2.51413 2.51274 2.51148 2.51036 2.50935 2.50844 2.50761 2.50688 2.50621 2.50561 2.50507 2.50458 2.50414 2.50374 2.50338 2.50306 2.50276 2.5025 2.50226 2.50204 2.50185 2.50167 2.50151 2.50137 2.50124 2.50112 2.50101 2.50091 2.50083 2.50075 2.50068 2.50061 2.50055 2.5005 2.50045 2.50041 2.50037 2.50034 2.5003 2.50027 2.50025 2.50023 2.5002 2.50018 2.50017 2.50015 2.50014 2.50012 2.50011 2.5001 2.50009 2.50008 2.50007 2.50007 2.50006 2.50006 2.50005 2.50005
6.18629 5.94648 5.76729 5.63038 5.52377 5.43941 5.37172 5.31673 5.27158 5.23417 5.2029 5.17657 5.15426 5.13523 5.11891 5.10486 5.09269 5.08212 5.0729 5.06484 5.05776 5.05153 5.04604 5.04118 5.03687 5.03305 5.02965 5.02662 5.02392 5.02151 5.01935 5.01742 5.01568 5.01413 5.01274 5.01148 5.01036 5.00935 5.00844 5.00761 5.00688 5.00621 5.00561 5.00507 5.00458 5.00414 5.00374 5.00338 5.00306 5.00276 5.0025 5.00226 5.00204 5.00185 5.00167 5.00151 5.00137 5.00124 5.00112 5.00101 5.00091 5.00083 5.00075 5.00068 5.00061 5.00055 5.0005 5.00045 5.00041 5.00037 5.00034 5.0003 5.00027 5.00025 5.00023 5.0002 5.00018 5.00017 5.00015 5.00014 5.00012 5.00011 5.0001 5.00009 5.00008 5.00007 5.00007 5.00006 5.00006 5.00005 5.00005
11.1866 10.9466 10.7673 10.6304 10.5238 10.4394 10.3717 10.3167 10.2716 10.2342 10.2029 10.1766 10.1543 10.1352 10.1189 10.1049 10.0927 10.0821 10.0729 10.0648 10.0578 10.0515 10.046 10.0412 10.0369 10.033 10.0296 10.0266 10.0239 10.0215 10.0193 10.0174 10.0157 10.0141 10.0127 10.0115 10.0104 10.0093 10.0084 10.0076 10.0069 10.0062 10.0056 10.0051 10.0046 10.0041 10.0037 10.0034 10.0031 10.0028 10.0025 10.0023 10.002 10.0018 10.0017 10.0015 10.0014 10.0012 10.0011 10.001 10.0009 10.0008 10.0007 10.0007 10.0006 10.0006 10.0005 10.0005 10.0004 10.0004 10.0003 10.0003 10.0003 10.0002 10.0002 10.0002 10.0002 10.0002 10.0002 10.0001 10.0001 10.0001 10.0001 10.0001 10.0001 10.0001 10.0001 10.0001 10.0001 10.0001 10.0
We plot the energy as a function of inverse temperature β for different particle numbers N. The log-log scale reveals the power-law behavior in different temperature regimes:
- High temperature (small β): Classical behavior E ∝ T
- Low temperature (large β): Quantum behavior dominated by zero-point energy
Each curve represents a different particle number, showing how bosonic statistics modify the energy compared to the classical case.
1fig = Figure(size = (400, 250), fontsize = 7)
2ax = Axis(fig[1, 1],
3 xscale = log10,
4 yscale = log10,
5 xlabel = "Inverse Temperature β",
6 ylabel = "Energy E",
7 title = "Energy of Bosonic Gas in Harmonic Trap")
8
9for (i, N) in enumerate([1, 5, 10, 20])
10 row = mat[i, :]
11 lines!(ax, 1:0.1:10, row, label = "N = $N")
12end
13Legend(fig[1,2], ax)
14fig
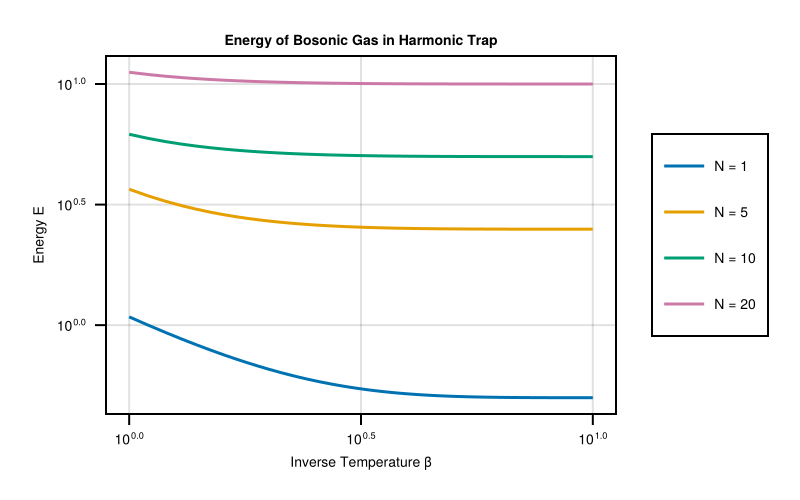
The results show several important features:
- Zero-point energy: Even at $T → 0 (β → ∞)$, the energy remains finite due to quantum fluctuations
- Bosonic enhancement: Higher particle numbers show deviations from classical behavior due to quantum statistics
- Temperature scaling: The energy follows different power laws in different temperature regimes
Version Information
1using InteractiveUtils
2InteractiveUtils.versioninfo()
1using Pkg
2Pkg.status()
This page was generated using Literate.jl.