Diagonalising 2D Schrödinger Equation
The text and method is based on the following sources:
- Youtube, 2D Schrodinger Equation Numerical Solution in PYTHON, (2022), Available at: https://youtu.be/DF1SnjXZcbM (Accessed: 6 March 2022).
- Alexvas, Discretization of Laplacian with boundary conditions, (2017), Available at: https://scicomp.stackexchange.com/q/25976 (Accessed: 6 March 2022).
- Thomas H. Pulliam, David W. Zingg., Fundamental Algorithms in Computational Fluid Dynamics, (2014), Springer.
using PyPlot, PyCall
using LinearAlgebra
using SparseArrays
using Arpack, KrylovKit
Two-dimensional box
$$ \hat{h}=\frac{-\hbar^{2}}{2 m} \nabla^{2}+V(\mathbf{r}, t). $$The box can have a homogeneous Dirichlet boundary condition, i.e., the wave function evaluated at the border must vanish, or periodic boundary conditions. There can be a potential $V$ in the box. So let us a meshgrid of $\mathbf{x}$ and $\mathbf{y}$ coordinates.
N = 100
L = 10.0
Δx² = (2*L/N)^2
function meshgrid(x, y)
X = [x for _ in y, x in x]
Y = [y for y in y, _ in x]
X, Y
end
x = LinRange(-L, L, N)
y = LinRange(-L, L, N)
X, Y = meshgrid(x, y);
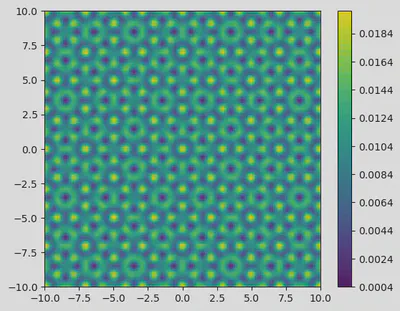
Potential
The potential is chosen to be eightfold rotation symmetric quasicrystal, centered on $\mathbf{r}=0,$ $$ V(\mathbf{r})=V_{0} \sum_{k=1}^{4} \cos ^{2}\left(\mathbf{G}_{k} \cdot \mathbf{r}\right) $$ where $V_{0}$ is the potential amplitude and the quantities $G_{k}$ are the lattice vectors of four mutually incoherent standing waves oriented at the angles $0^{\circ}, 45^{\circ}, 90^{\circ}$, and $135^{\circ}$, respectively. The lattice vectors have norm $\left|G_{k}\right|=\pi / a$.
function get_potential(x, y, V₀)
return V₀*(cos(pi*x)^2 + cos(pi*√2/2*(x+y))^2 + cos(pi*y)^2 + cos(-pi/(√2)*(x-y))^2)
end
V = get_potential.(X,Y, 0.005)
fig = figure(figsize=(6.2,5))
contourf(X, Y, V, 50)
colorbar()
Units
The Schrödinger equation is given by $$ \left[\frac{-\hbar^{2}}{2 m} \nabla^{2}+V(\mathbf{r})\right] \psi(\mathbf{r}) = E\psi(\mathbf{r}),$$ Let us use the lattice spacing $a$ and the corresponding recoil energy $E_r = \pi^2\hbar^2/2ma^2$ as the space and energy units, respectively, such that we have $$ \left[\frac{-\hbar^2}{2mE_ra^2} \tilde{\nabla}^{2}+\frac{V(\mathbf{\tilde{r}})}{E_r}\right] \psi(\mathbf{\tilde{r}}) = \left[\frac{-1}{\pi^2} \tilde{\nabla}^{2}+\tilde{V}_{0} \sum_{k=1}^{4} \cos ^{2}\left(\tilde{\mathbf{G}}_{k} \cdot \tilde{\mathbf{r}}\right)\right] \psi(\mathbf{\tilde{r}}) = \tilde{E}\psi(\mathbf{\tilde{r}}), $$ where $|\tilde{\mathbf{G}}_{k}|=\pi$, $\tilde{\mathbf{r}} = \frac{\mathbf{r}}{a}$, and $\tilde{E}=\frac{E}{E_r}$.
Discretize in one dimension
$$ \frac{d^2 \psi}{dx^2} \approx \frac{\psi_{i+1}-2\psi_i + \psi_{i-1}}{\Delta x^2}.$$Dirichlet boundary conditions
Suppose we have $M=4$ interior points and $a$ and $b$ two boundary points, a mesh with four interior points $\Delta x=2L /(M+1)$, represented as follows \begin{align*} &\qquad \ \ a \ \ \ \ 1 \ \ \ \ 2 \ \ \ \ 3 \ \ \ \, 4 \ \ \ \ b \\\ &x=-L \ - \ - \ - \ - \ \ L \end{align*} We impose Dirichlet boundary conditions, $u(-L)=u_{a}, u(L)=u_{b}$ and use the centered finite difference approximation at every point in the mesh. We arrive at the four equations: \begin{align*} \left(d_{x x} u\right)_{1} &=\frac{1}{\Delta x^{2}}\left(u_{a}-2 u_{1}+u_{2}\right) \qquad \left(d_{x x} u\right)_{2} =\frac{1}{\Delta x^{2}}\left(u_{1}-2 u_{2}+u_{3}\right) \\\\\\ \left(d_{x x} u\right)_{3} &=\frac{1}{\Delta x^{2}}\left(u_{2}-2 u_{3}+u_{4}\right) \qquad \left(d_{x x} u\right)_{4} =\frac{1}{\Delta x^{2}}\left(u_{3}-2 u_{4}+u_{b}\right) \end{align*} Introducing \begin{align*} \vec{u}=\left( \begin{array}{c} \psi_{1} \\\ \psi_{2} \\\ \psi_{3} \\\ \psi_{4} \end{array} \right) \quad (\overrightarrow{b c})=\frac{1}{\Delta x^{2}} \left( \begin{array}{c} \psi_{a} \\\ 0 \\\ 0 \\\ \psi_{b} \end{array} \right) \quad A=\frac{1}{\Delta x^{2}} \left( \begin{array}{rrrr} -2 & 1 & & \\\ 1 & -2 & 1 & \\\ & 1 & -2 & 1 \\\ & & 1 & -2 \end{array} \right) \end{align*} we can rewrite in matrix form as \begin{align*} \frac{d2 \psi}{dx2} =\frac{1}{\Delta x^{2}}D= A \vec{\psi}+(\overrightarrow{b c}) \end{align*}
Periodic boundary conditions
This subsection has to be tested and worked out. First try did not work.
Suppose we have $M=8$ points on a linear periodic mesh, represented as follows \begin{align*} &\cdots \ \ \ 7 \ \ \ \ 8 \ \ \ \ \ \ a \ \ \ \ 1 \ \ \ \ 2 \ \ \ \ 3 \ \ \ \ 4 \ \ \ \ b \ \ \ \ 1 \ \ \ \ 2 \ \ \ \cdots \\\ &x= \ - \ \ - \ \ -L \ \ - \ \ - \ \ - \ \ - \ \ L \ \ - \ \ - \end{align*} where we have that $\psi(L)=\psi(-L)$. It can be shown that the matrix representation is modified by \begin{align*} \frac{d2 \psi}{dx2} =\frac{1}{\Delta x^{2}}D_p=\frac{1}{\Delta x^{2}} \left( \begin{array}{rrrr} -2 & 1 & & 1 \\\ 1 & -2 & 1 & \\\ & 1 & -2 & 1 \\\ 1 & & 1 & -2 \end{array} \right) \end{align*}
Discretize in two dimensions
$$ \left( \begin{array}{rrrr} \psi_{11} & \psi_{12} & \cdots & \psi_{1N} \\\\\\ \psi_{21} & \psi_{22} & \cdots & \psi_{2N} \\\\\\ \vdots & \vdots & \ddots & \vdots \\\\\\ \psi_{N1} & \psi_{N2} & \cdots & \psi_{NN} \end{array} \right) \rightarrow \left( \begin{array}{c} \psi_{11} \\\\\\ \psi_{12} \\\\\\ \vdots \\\\\\ \psi_{NN} \end{array} \right) $$$$ \frac{\partial^2 \psi}{\partial x^2} = \frac{1}{\Delta x^{2}} I \otimes D = \frac{1}{\Delta x^{2}} \left( \begin{array}{rrr} D & & \\\\\\ & \ddots & \\\\\\ & & D\end{array} \right) $$$$ \nabla^{2} = \frac{\partial^2 \psi}{\partial x^2} + \frac{\partial^2 \psi}{\partial y^2} = \frac{1}{\Delta x^{2}} (I \otimes D + D \otimes I) = \frac{1}{\Delta x^{2}} D\oplus D $$where $\oplus$ is the Kronecker sum, and we used that we discretized space as a squared grid, i.e. $\Delta x^{2}=\Delta y^{2}$.
Hamiltonian
$$ \left[-\frac{1}{\pi^2}(D \oplus D) + \Delta x^2 \tilde{V} \right] \psi = \left( \Delta x^2 \tilde{E}\right) \psi, $$$$ \hat{h} = -\frac{1}{\Delta x^{2}\pi^2} D \oplus D + \tilde{V} $$such that the corresponding eigenvalues $\tilde{E}$ are in units of recoil energy $E_r$. Let $T=-\frac{1}{\Delta x^{2}\pi^2} D \oplus D$ and $U = V$
diag = ones(N); # vector of ones
diags = Vector([diag[begin:end-1], -2*diag, diag[begin:end-1]]); # vector of vectors of the diagonals
D = sparse(Tridiagonal(diags...)) # creates the discretised 2nd derivative
T = -1/(Δx²*pi^2) * (kron(D, sparse(I,N,N)) + kron(sparse(I,N,N), D)) #N**2 x N**2 matrix
U = spdiagm(reshape(V, N^2))
H = T+U;
Here we used the package SparseArrays.jl to make the computations faster. Sparse arrays are arrays that contain enough zeros that storing them in a special data structure leads to savings in space and execution time, compared to dense arrays.
Eigenvectors and eigenvalues
Now that we constructed our discretized Hamiltonian we can just exactly diagonalize our Hamiltonian to find the eigenvalues and eigenvector. We shall to this with the package Arpack.jl which is a Julia wrapper to a FORTRAN 77 library designed to compute a few eigenvalues and corresponding eigenvectors of large sparse or structured matrices, using the Implicitly Restarted Arnoldi Method (IRAM) or, in the case of symmetric matrices, the corresponding variant of the Lanczos algorithm. Both are classified as Krylov subspace based algorithms (see wikipedia). It is used by many popular numerical computing environments such as SciPy, Mathematica, GNU Octave and MATLAB to provide this functionality.
We use the eigs function where nev specifies how many eigenvalues and eigenvectors we want and which specifies the type of eigenvalues to compute. For my purposes I only need the ground state wave function.
Alternatively, one could use KrylovKit.jl, a native Julia package collecting a number of Krylov-based algorithms for linear problems, singular value and eigenvalue problems and the application of functions of linear maps or operators to vectors. With KrylovKit.jl I manage to find better results if when I increase the number of point $N$. My theory is that it, as black box solver, uses another method above a certain threshold $N^*$, whereas Arpack.jl sticks to the same method and hence gives worse results.
# eigenvalues, eigenvectors = eigs(H, nev=1, which=:SM);
_, vecs, _ = eigsolve(H, 1, :SR);
# vecs[1]
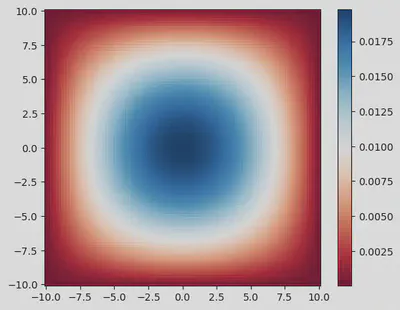
As we constructed the Hamiltonian to be a $N^2 \times N^2$ so that $\psi$ could be a vector, we have to reshape the eigenvectors back to a $N \times N$ matrix.
function get_e(n::Int64)
return reshape(vecs[1]', N, N)
end;
figure(figsize=(6.2,5))
pcolormesh(X, Y, get_e(0)^2, cmap=:RdBu)
colorbar()
# contourf(X, Y, get_e(0)^2, 100)
Summary
using PyPlot, PyCall
using LinearAlgebra
using SparseArrays
using Arpack, KrylovKit
function meshgrid(x::LinRange{Float64, Int64}, y::LinRange{Float64, Int64})::Tuple{Matrix{Float64}, Matrix{Float64}}
X = [x for _ in y, x in x]
Y = [y for y in y, _ in x]
X, Y
end
function QC(x::Float64, y::Float64, V₀::Float64)::Float64
return V₀*(cos(pi*x)^2 + cos(pi*√2/2*(x+y))^2 + cos(pi*y)^2 + cos(-pi/(√2)*(x-y))^2)
end
function free(x::Float64, y::Float64, V₀::Float64)::Float64
return V₀*(0*x+0*y)
end
function PC(x::Float64, y::Float64, V₀::Float64)::Float64
return V₀*(sin(pi*x)^2+sin(pi*y)^2)
end
function eigenfunctionDBCArpack(V::Matrix{Float64}, L::Float64, N::Int64)
Δx² = (2*L/N)^2
# creates the discretised 2nd derivative
D = sparse(Tridiagonal(ones(N-1), -2*ones(N), ones(N-1)))
# N**2 x N**2 matrix
T = -1/(Δx²*pi^2) * (kron(D, sparse(I,N,N)) + kron(sparse(I,N,N), D))
U = spdiagm(reshape(V, N^2))
H = T + U;
_, eigenvector = eigs(H, nev=1, which=:SM);
return reshape(eigenvector', N, N)
end
function eigenfunctionDBCKrylov(V::Matrix{Float64}, L::Float64, N::Int64)
Δx² = (2*L/N)^2
# creates the discretised 2nd derivative
D = sparse(Tridiagonal(ones(N-1), -2*ones(N), ones(N-1)))
# N**2 x N**2 matrix
T = -1/(Δx²*pi^2) * (kron(D, sparse(I,N,N)) + kron(sparse(I,N,N), D))
U = spdiagm(reshape(V, N^2))
H = T + U;
_, vecs, _ = eigsolve(H, 1,:SR)
# _, eigenvector = eigs(H, nev=1, which=:SM);
return reshape(vecs[1]', N, N)
end
# function eigenfunctionPBC(V::Matrix{Float64})
# Δx² = (2*L/N)^2
# # creates the discretised 2nd derivative
# D = sparse(Tridiagonal(ones(N-1), -2*ones(N), ones(N-1)))
# D[1, end] = 1.0
# D[end, 1] = 1.0
# # N**2 x N**2 matrix
# T = -1/(Δx²*pi^2) * (kron(D, sparse(I,N,N)) + kron(sparse(I,N,N), D))
# U = spdiagm(reshape(V, N^2))
# H = T + U;
# N = size(V)[1]
# # creates the discretised 2nd derivative
# D = sparse(Tridiagonal(ones(N-1), -2*ones(N), ones(N-1)))
# _, eigenvector = eigs(H, nev=1, which=:SM);
# return reshape(eigenvector', N, N)
# end
V₀ = 0.8
L = 50.0
Δx² = 0.1
N = Int64(div(2L, Δx²))
X, Y = meshgrid(LinRange(-L, L, N), LinRange(-L, L, N));
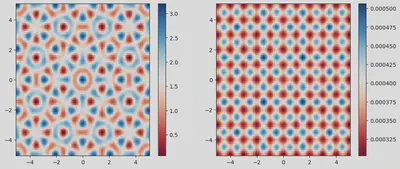
V = QC.(X, Y, V₀)
ef = eigenfunctionDBCKrylov(V, L, N)
fig, axes = subplots(nrows=1, ncols=2, figsize=(12, 5))
im1 = axes[1].pcolormesh(X[450:550,450:550], Y[450:550,450:550], V[450:550,450:550], cmap=:RdBu)
colorbar(im1, ax=axes[1])
im2 = axes[2].pcolormesh(X[450:550,450:550], Y[450:550,450:550], ef[450:550,450:550]^2, cmap=:RdBu)
colorbar(im2, ax=axes[2])
PyObject <matplotlib.colorbar.Colorbar object at 0x000000006E89FF40>
# @pyimport matplotlib.animation as anim
# using Base64
# fig = figure(figsize=(6.2,5))
# function make_frame(i)
# V₀ = 0.02*i
# L = 10.0
# N = 150
# X, Y = meshgrid(LinRange(-L, L, N), LinRange(-L, L, N));
# V = QC.(X, Y, V₀)
# ef = eigenfunctionDBC(V)
# pcolormesh(X, Y, ef^2, cmap=:RdBu)
# end
# withfig(fig) do
# myanim = anim.FuncAnimation(fig, make_frame, frames=20, interval=200)
# myanim[:save]("test2.mp4", bitrate=-1, extra_args=["-vcodec", "libx264", "-pix_fmt", "yuv420p"])
# end
# function showanim(filename)
# base64_video = base64encode(open(filename))
# display("text/html", """<video controls src="data:video/x-m4v;base64,$base64_video">""")
# end
# showanim("test2.mp4")